同梱可能な商品をカートに入れて購入すると、複数購入しても送料は追加されません。
1
2
3
4
5
6
7
8
9
10
同梱可能な商品は
現在カートに入っていません。
| メーカー/原産地 | 国内 | 商品の状態 | 新品 |
|---|---|---|---|
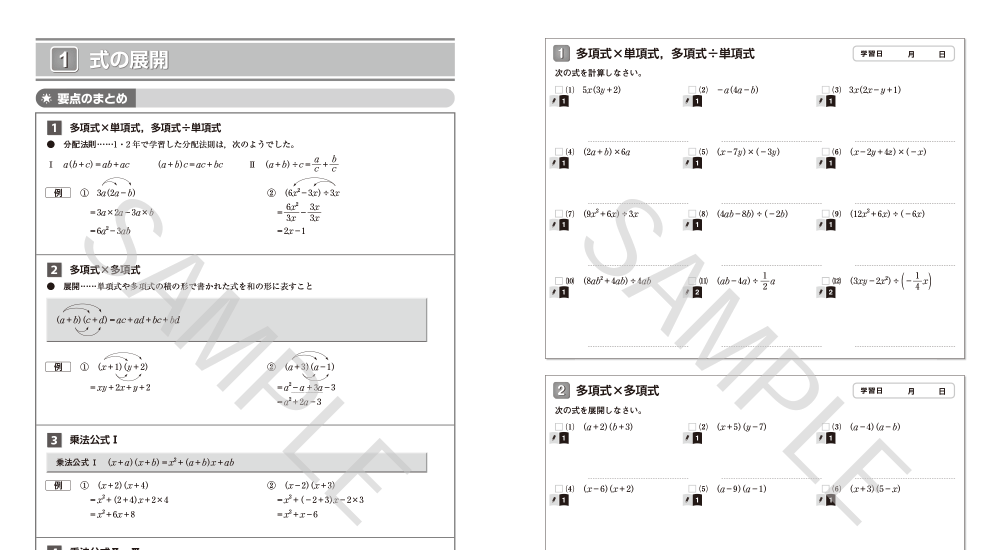
| 発送国 | 国内 (日本) | ||
| 材料/素材 | ご覧下さりありがとうございます。画像の後に、商品説明がございます。 【即決】ご入札いただければすぐにお取引が成立します。 ★商品説明★ UNIFIED MODERN MATHEMATICS 現代の統合数学 中学校編 全6巻+解答編 全巻揃 代表著者・H.F.フェア 編訳・日本数学教育学会 監訳・大野清四郎 宇都宮大学教授 佐々木元太郎 滋賀大学教授 玉木和之 東京都荒川区立日暮里中学校長 新教社 発行 昭和51年 初版 函入 カバー付 約22x15.5cm ※絶版 第1巻 上 263P 第1巻 下 307P 第1巻 解答編 48P 第2巻 上 267P 第2巻 下 203P 第2巻 解答編 第3巻 上 199P 第3巻 下 211P 第3巻 解答編 44P SSMCISのプログラムによる数学の教科書についての日本における翻訳として、先進国における数学教育を新体系として惜しみなく公開したもの。 中学校編と題されてはいますが、算数から現在の高校数学の内容までを含んでいます。 全6冊、解答編も揃った完全セット、大変貴重な資料本です。 【訳者の言葉】より われわれがSSMCISの活動を直接的に身近なものとしたのは，昭和47年の２月に秋月康夫先生から, SSMCISのリポート(Mathematics Education in Europe and Japan)を参考にして研究するようにとの示唆をいただいてからである。われわれは，早速，このリポートを翻訳研究し，先進各国の数学教育改善の助向をさらに広く把握したが，それと同時に, H.F.フェア教授のご好意により, SSMCISのプログラムによる教科書についての日本における翻訳を許され，その訳出にあたったのである。 たまたま，昭和49年の11月に, ICMI-JSMEの東京会議に来日されたH.F.フェア教授と懇談の機会を得，この教科書の全訳出版について全面的な承認と激励をいただくとともに，株式会社新数社のなみなみならぬご厚意により発刊の運びになったことは，われわれの衷心より感謝するところである。 SSMCIS (Secondary School Mathematics Curriculum Improvement Study:中等学校数学教育課程改善研究会）は，アメリカのコロンビア大学内に設置された研究会で, H.F.フェア教授を主たる指導者とし1965年以来，数学を今日的な観点―集合，関係と写像，代数的櫛造，位相構造の基本的な考えにもとづく―から一つの体系を考え，明日の社会に生きる今日の生徒の知性の育成を第一の目標とし，国内および諸外国の中等学校の数学教育の実態を熟視しながら，数多くの実験を経て，今後の望ましい数学の教科書および教師のための指導書の作成を推進してきている。 この教科書を見ると，内容の集約精選は慎重かつ果断であり，生徒の発達段階を十分に配慮して教材が展開され，しかも，全体を通じて現代の数学の精神が脈々と流れて，21世紀をめざした数学教育ヘアプローチする姿がひしひしと感じられる。このことは，わが国におけるこれからの数学教育に，この上もない刺激を与え，方向を示唆するものであると確信する。 SSMCISのプログラムによる教科書は，すでにⅠ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵと完成されているが，今回出版するのは，そのうちコースⅠ,Ⅱ,Ⅲである。これらは,わが国の中学佼の生徒に相当するもので，コースＩを第１巻(上・下)，コースⅡを第２巻,(上・下)，コースⅢを第３巻(上・下)としてまとめたものである。 ご承知のように，アメリカのこの種の教科書は，わが国のそれと異なり，説明は懇切であり，記述はていねいである。これは，特にSSMCISにおいて強調されているところの数学の学習に対する基本的な考え， 教師と生徒による力強い知的参加 生徒同志，教師と生徒との間の活発な対話と討論 教師の助言のもとでの生徒自身による積極的な学習 などの実践を可能にし，その効果を期待するための配慮からでもある。 この教科書に盛られた内容もさることながら，その展開の方法からも，われわれは多くのものを学びとることができよう。このような観点からも，本書の活発な利用と実践を切望してやまない。 終わりに，本書の分担訳出に多大の労をいただいた数学科教育課程研究委員会の各委員，本書の刊行に対し，積極的な意欲と万全の配慮を賜った新数社の諸氏に満腔の謝意を表するしだいである。 【序文】 これまでは，数学というものは，算数・代数・幾何・微積分学などの別々の部門を学習するものと，考えられてきた。そして，これらの部門は１年あるいは，それ以上にわたって別々に学習された。 今日の数学は，それとは違って,すべての古典的な部門に共通している系統，または構造の集合と見なされている。これらの系統においては,集合・操作（演算）・写像，および関係の諸概念が基礎である。 数学をこのような観点で見るとき，この学科は，統一的なものに感じられ，その学習はいっそう効果的なものになる。 この（教科）書は，基本的な構造を築くことをめざして，着手されるシリーズのはじめのコースである。この本の中で，算数的な演算を持つ系の性質を調べるために，小学校で学習した算数を，新しい時計の算数といっしょにして吟味する。 続いて起こる，すべての学習を援助するために，集合に関する用語と写像に関係した用語とを導入する。また，群と呼ばれる構造を明らかにし，拡張した構造をもつ整数の集合に発展させる。 さらに，点の写像をつくり，直線上や格子状の直線の中で，点と数とを関係づける。 このようにして，しだいに算数・代数，および幾何を統合的な学習に融合していくことになる。なお，これらにつけ加える学習としては，確率と数論とを考慮している。 《原著者紹介》 「現代の統合数学第１巻」は,中等学校数学カリキュラムの改善研究のために，次の方々の協力を得て作成された。 Gustave Choquet パリ大学（フランス） Ray Cleveland キャルガリー大学（カナダ） John Downes エモリ一大学 Howard Ｆ. Fehr コロンビア大学教員養成学部 James Fey コロンビア大学教口養成学部 Abraham Glicksman ブロンクス科学高等学校（ニューヨーク） Vincent Haag フランクリン・マーシャル大学 Thomas Hill オクラホマ大学 Peter Hilton コーネル大学 Julius Hlavaty 全米数学教師協議会 Michael Hoban CFG アイオナ大学（ニューヨーク） Meyer Jordan ニューヨーク市立大学 Burt Kaufman 南部イリノイ大学 Erik Kristensen オルフス大学（デンマーク） Howard Levi ニューヨーク市立大学 Edgar Ray Lorch コロンビア大学 Lennart RAde シャルマー科学技術研究所（スウェーデン） Harry Rudertnan ハッター大学高等学校（ニューヨーク） Harry Sitomer コロンビア大学教員養成学部 Hans-Georg Steiner カールスルーエ大学（西ドイツ） Marsliall H. Stone マサチューセッツ大学 Stanley Taback ウォルデン中等学佼（ニューヨーク） Ｈ. Laverne Thomas オニオンタ州立大学（ニューヨーク） Albert Ｗ. Tucker プリンストン大学 Bruce Vogeli コロンビア大学教員養成学部 【はしがき】 数学の，算数，代数，幾何，および解析と呼ばれる研究の分科への古典的な分け方は，数学の発達の歴史的な反映である。数学のこの分け方と同じ分け方が，わが国の学校で生徒へ数学を提示するやり方になってきたのは自然のことである。しかし，最近の150年間に，数学者たちは，数と空問の本質についてより深い理解に達し，伝統的な分科の根底にある根本的な概念を明らかにしてきた。これらのアイディアは，すでに算数の学習で出会ってきた集合；関係，すなわち，一つの共通な性質によって一つの集合の元を対応させること；一つの集合の元をもう一つの集合の元に対応させる写像または関数；および二つの整数（0と自然数をいう）の加法や乗法のような二項演算のそれらである。 これらの基礎的なアイディアの助けにより，論理と呼ばれる推論を用いて，伝統的な数学のすべての分科は，新しく発見された数学とともに，最近50年間に数学を一つのものとして統合するように再構成された。大学およびそれよりも高度のレベルでは，この統合は，パリに本部をもつブルバキと呼ばれる有名な国際的なグループの数学者たちによってなされた。現代の統合された，または今日的といわれるのは，この機構である。 この教科書において，一つの統合された教科として数学を学習することができよう。もちろん，代数，幾何，算数および数論があるが，それらのすべてが集合，論理，関係，関数，および演算を一般的に用いることによって互いに関連づけられている。そこには,現在の生活場面への数々の数学の応用が見られる。 この教材は，生徒および読者が研究し，かつ学習するために書かれたものであり，練習問題は，学習する概念とアイディアを理解するためのものである。 教室の授業では，討論と真剣な思考とを通してこの教材を学習し，明確でない点をはっきりさせるには,別の取り組み方を探究することによって,数学と科学のさらに進んだ研究に役立つ健全な知識を発達させることができるのである。 H. F.フェア 【目次】 ●1・上 1章 有限数体系 ジェーン・アンダーソンの算数 時計の算数 （Z12,+）と（Ｗ,+） カレンダーの算数 開いた文 新しい時計 回転 時計の算数での減法 時計の算数の乗法 （Ｗ,・）と時計の乗法の比較 時計の算数の除法 時計の算数 における逆元 結合法則と分配法則 まとめ 2章 集合と演算 数の順序対とそれに対応させる数 演算とは何か いろいろな演算による計算 開いた文 演算の性質 簡約法則 ２つの演算系 群とは何か まとめ 3章 数学的写像 対応と写像 整数の集合Ｗの写像 時計の数について の写像 数列 写像の合成 逆写像と恒等写像 ＷからWへの特別な写像 まとめ 4章 整数と加法 はじめに いくつかの新しい数 整数と反数 （Ｚ，+）の性質 整数と直線上の平行移動 （Ｚ,+）についての減法 反数の加法としての減法 （Ｚ,+）における方程式 簡約法則 整数の順序づけ 絶対値 まとめ 5章 確率と統計 はじめに 実験についての議論 生徒による実験 事象の確率 チャンスのゲーム 同様に確からしい結果 ある種の写像 樹形図による計算 予習 研究問題 統計的資料 表による資料の提示 度数ヒストグラムと累積度数ヒストグラム まとめ 6章 整数の乗法 演算系（W,+）と（Ｚ，・） Ｚにおける乗法 正の整数と負の 整数の乗法 ２つの負の整数の積 分配法則と整数の乗法 膨張変換と整数の乗法 まとめ 7章 平面上の格子点 格子点と順序対 ＺｘＺ上の条件とそのグラフ 解集合の交わりと結び 絶対値条件 格子点ゲーム 格子点の集合とＺからＺへの写像 空間の格子点 平行移動とＺｘＺ 膨張変換とＺｘＺ いくつかの特別な写像とＺｘＺ まとめ ●1・下 8章 集合と関係 集合 集合の相等と部分集合 全体集合，部分集合およびべン図 結び，交わりおよび補集合 デカルト積：関係 関係の性質 同値類と分割 まとめ 9章 平面の変換 方法を知ることと行うこと 直線についての対称変換 直線射線線分 垂直の線 同じ端点をもつ射線 点対称変換 平行移動 回転 まとめ 10章 線分・角・等長変換 はじめに 直線射線線分 平面と半平面 線分の長さ 中点と分点 座標を用いての等長変換の拡張 座標と平行移動 垂直な直線 点および直線についての対称変換を座標を用いて表す 角とは何か 角の測定 コンパス(羅針儀)の読みとり さらに角について 角と直線についての対称変換 角と点対称変換 角と平行移動 三角形の角の測度の和 まとめ 11章 初等的な数論 (Ｎ,+)と(Ｎ,・) 整除性 繁数と合成数 素因数分解 エラトステネスの篩 素数の数について ユークリッドの互除法 まとめ 12章 有理数 Ｗ,ＺとＺ7 整数の逆数 Ｚ∪ＺからＱへの拡張 (Ｑ，・) (Ｑ，・)の性質 有理数の除法 有理数の加法 有理数の減法 有理数の順序 小数 無限循環小数 小数と有理数の順序 まとめ 13章 有理数の若干の応用 有理数と膨張変換 小数についての計算 比と比例 比例の用法 百分率の意味 百分率に関する問題の解決 帯グラフ,円グラフ,棒グラフで表される資料 平行移動と群 平行移動の応用 まとめ 14章 アルゴリズムとそのグラフ 数学的な処理の計画 分岐を合むアルゴリズムのフローチャート 反復アルゴリズム 手順の中断と中断基準 ●2・上 1章 数学的な言葉と証明 はじめに 数学的な文章 結合詞：かつ，または 条件命題と複合条件命題 量化された命題 等式に対する置き換えの原理(ＳＰＥ) 推論 数学的直接証明法 間接証明 まとめ 2章 群 群の定義 非可換群 置換の続き 関数記号 いろいろな記法 群についてのいくつかの定理 同形写像 まとめ 3章 公理的アフィン幾何入門 前おき 公理 公理からの論理的結果 公理の幾何学的でないモデル 公理のその他のモデルー有限と無限 平行線の同値類 平行投影 ベクトルー直観的な導入 まとめ 4章 体 体とは何か いくつかの体の定理 0について 体における減法と除法 体における分数 体における順序 順序体の数 （Ｑ,+，・，＜）における方程式と不等式 ２次方程式の解法 まとめ 5章 実数系 方程式 x^2=2 測定の手続き 線分の長さ ３つの場合の説明 実数系 実数系の性質 実数の順序 無理数の計算 まとめ 6章 座標幾何学 はじめに 公理４，直線座標系の一意性 公理５，一直線上の２つの座標系の関係 線分，射線，中点 公理６，平行投影と直線の投影 平面座標系 直線の方程式 直線の交わり 三角形と四角形 ピタゴラスの性質 平面直交座標系 まとめ ●2・下 7章 実関数 数学的写像 実関数の性質 実関数を表すこと 実関数の合成 実関数の逆元 [ｆ+ｇ]と［ｆ-ｇ］ [ｆ・ｇ]と［ｆ/ｇ] 平方根と立方根の関数 まとめ 8章 記述統計 導入 データの集合とそのグラフ表現の例 記号Σと総和 算術平均,その計算と性質 散布度 分散および標準偏差の簡単な計算 チェビシエフの不等式 まとめ 9章 平面の変換 変換とは何か 直線についての対称変換 平行移動 回転と半回転 合成された等長変換，ずらし対称変換 ３つの対称変換についての定理 同じ向きの等長変換 等長変換の群 等長変換，合同および相似 他の変換：膨張変換および相似性 まとめ 10章 長さ,面積，体積 はじめに 集合についての測度 線分の長さ 長方形領域の面秘 直方体の体積 三角形領域の面積 平行四辺形領域と 台形領域の面積 その他の領域の面積 円周とπ 円領域の面積 まとめ 付録 質点 質点 記号と処理 質点についての公理 定理 もう１つの定理 定義の使用 空間における質点と定理 まとめ ●3・上 1章 行列への入門 行列とは何か 複雑な状況の記述に行列を使うこと 行列の演算 行列とコード化 された通信 行列と変換 推移行列 まとめ 2章 １次方程式と行列 連立１次方程式 ピボット（pivot）法 連立１次方程式の解き方（続き） 同時１次方程式 １次方程式の行列表示から導かれた行列の積 逆行列 文章題 まとめ 3章 行列の代数 行列の世界 行列の加法 スカラーによる乗法 行列の乗法 Ｍ，における乗法の逆元 2×2行列の環 2×2行列の体 まとめ 4章 グラフと関数 条件とグラフ 平面上の領域と平行移動 関数と条件 関数と方程式の解 関数についての演算 有界関数と漸近線 まとめ 5章 組合せ数学 はじめに 数え方の原理と順序 ベキ集合 与えられた大きさの部分集合の個数 二項定理 数学的帰納法 まとめ ●3・下 6章 確率 はじめに 結果の集合と事象 確率測度 一様確率測度 いままでの反省 さきの見通し まとめ 7章 多項式と有理関数 多項式関数 多項式の次数 多項式の加法；(P,+) 多項式関数の乗法；(P,+，・) 多項式関数の除法 多項式の因数と因数定理 ２次関数と方程式 有理関数 実有理関数についての演算 まとめ 8章 円関数 有向角 標準位置 角の円関数 実数の円関数 度数法，弧度法および角の加法 いくつかの特別の角 円関数のグラフ 余弦定理と正弦定理 まとめ 9章 初等空間幾何 空間幾何と平面幾何 空間における平面 空間における平行線と平面 ３次元空間における幾何の演繹的な入門 ３次元空間における座標系 空間における直線と平面の垂直線 空間における直交座標系 空間における距離 空間における曲面 まとめ ★状態★ 昭和51年のとても古い本です。 函の外観は経年ヤケしみ、色むら、第3巻の裏側にはがれ（約3ｘ3cm）あり。 カバー付き表紙外観は通常保管によるスレ程度、天小口に経年ヤケしみあり、 本文はパラパラとめくって目立った書込み・線引無し、 問題なくお読みいただけると思います。（見落としはご容赦ください） ＜絶版・入手困難本＞オークションにも滅多に出ない、貴重な全巻セットです。 古本・品にご理解のある方、この機会にぜひ宜しくお願いいたします。 ★お取引について★ ■商品が到着しましたら、必ず「受取連絡」のお手続きをお願い申し上げます。 ■品です。それなりの使用感がございます。 モニタのバックライトの作用により、写真画像は実際よりきれいに見えがちです。 ■絶版・廃盤、一般の書店で販売されない限定販売、 書店や出版社で在庫切れである、またはその他の理由により、 定価に関係なく相場に合わせて高額となる場合があります。 ■「かんたん決済支払明細」の画面を保存・印刷することで領収書に代えさせて頂きます。 領収書に出品者の押印がご必要の場合、「受取連絡」にて代金領収後に別送いたしますので、 取引ナビにて別途ご依頼ください。 ■ＰＣよりの出品です。携帯フリマサイトのようにすぐにご返信はできかねます。 ■かんたん決済支払期限が切れた場合、落札より一週間以内に連絡が取れない場合、 落札者都合にてキャンセルいたします。 （ヤフオク！システムより自動的に「非常に悪い」評価が入ります。これは出品者からの評価ではありません。） ■土・日・祝日は、取引ナビでの応答・発送をお休みしております。 他に連絡・発送のできない日は自己紹介欄に記載しております。 ■万一、商品やお取引に問題があった場合は、いきなり評価ではなく、 取引ナビにてご連絡ください。 誠実に対応いたしますので、ご安心いただけますと幸いです。 ■上記の点をご了承頂ける方のみ、 ご入札くださいますようお願い申し上げます。 ★商品の状態について★ ヤフオク！の定める基準をもとに、出品者の主観により判断しています。 以下は公式ページより選択の目安より転載します。 新品、未使用…未開封の新品、または購入から時間がたっていない一度も使用していない商品 未使用に近い…ではあるが数回しか使用しておらず、傷や汚れがない 目立った傷や汚れなし…品。よく見ないとわからないレベルの傷や汚れがある やや傷や汚れあり…とわかるレベルの傷や汚れがある 傷や汚れあり…品。ひとめでわかるレベルの大きな傷や汚れがある 全体的に状態が悪い…品。大きな傷や汚れや、使用に支障が出るレベルで不具合がある。ジャンク品など。 |
||
| 決済方法 | VISA, MasterCard, AMEX, JCB card, PayPal, LINE Pay, PayPay, コンビニ決済, Suica決済, あと払い(ペイディ), 銀行振り込み, ネットバンキング, Qサイフ | ||
| A/S情報 | A/Sセンターおよびメーカーまたは販売者にご連絡ください。 | ||
| 返品/交換 | 商品ページ上の詳細やお知らせ・ご注意を参考してください。 | ||
![新課程 [大学入試最頻出 42] ベーシックスタイル 数学演習III・C〔複素数平面，式と曲線〕 受験編 ー 内容を見る｜チャート式の数研出版](http://www.chart.co.jp/wp_item/wp-content/uploads/2024/04/24196_naiyou1.jpg)
-
商品満足度
4.5 -
採点分布
-
5つ★
86%
-
4つ★
6%
-
3つ★
8%
-
2つ★
0%
-
1つ★
0%
-
5つ★
項目別評価
- つけ心地
-
満足です
93%
- 発色の良さ
-
満足です
93%
- 盛れ感
-
満足です
91%
- つけ心地
-
- 満足です
-
93%
- イマイチ
-
7%
- 発色の良さ
-
- 満足です
-
93%
- イマイチ
-
7%
- 盛れ感
-
- 満足です
-
91%
- イマイチ
-
9%
-
4 5zsw*** 2024-12-23 19:42:47
ペアリングも簡単で、音質も非常に良い！！
-
5 5sdk*** 2024-12-21 14:42:47
今使っている物が、そろそろ寿命な感じなので購入しました。
軽くて、良いです。
見た目もかっこいいです。
皆さんのレビューを見て、音は大きいのかな…と思っていましたが、ウチの現役より静かで気に入りました！ -
4 5uyt*** 2024-12-22 18:42:47
シンプルですが、手触りも色合いも良く、期待以上で大満足です。
-
4 5cyn*** 2024-12-19 17:42:47
今までのナイロンタオルに比べあきらかに、爽快感が増しました。値段は高いですが納得です
-
5 5xra*** 2024-12-20 13:42:47
BSアンテナを取り付けたのですが、分波器が必要とは知らず見る事が出来ませんでした。
依頼をしてからの配送も早く、とても助かりました。 -
4 5qvv*** 2024-12-18 15:42:47
到着まで時間はかかりましたが、書いてあったので待てました。
ニキビが翌日には小さくなっていて効果を感じました。 -
4 5vim*** 2024-12-16 14:42:47
普段は商品によってSかMサイズ。
こちらでは大きめな方がよさそうな意見を見かけたので、9号の品を試着しようと3点注文。
結果、大きく感じて7号と交換してもらうことに。
7号でぴったりでした。
こちらの商品はウエストをリボンでおされられるので9号でも最終的にはどうにかなりそうでしたが、
着比べてみたら、ドレスなのでやはりピッタリのサイズの方が綺麗に見えます。
ショップのイチオシ商品
399 商品販売中 ショップへ
こちらはどうですか?PR
- 四谷快談！全巻セット
- 11,000円
- 4.9(811)
- ヤンマ産業 会津木綿タックスカート プラス丈
13,200円- 11,220円
- 4.6(628)
- 41PX製 ARP556 2.0陽炎2型E搭載｢EVO｣
- 53,500円
- 4.8(6,374)
- 【都屋】15 輪島塗 輪島 五島屋謹製「汁椀」5客 共箱 高さ 約6.5㎝ 幅 約12㎝ 木製 吸物椀 煮物椀
12,200円- 10,370円
- 4.6(628)
- ヤマハ スポーツ HX90 純正タンク 品 当時物 北海道 札幌市より
8,900円- 7,565円
- 4.6(628)
- グレンロセス 1987
- 16,900円
- 4.6(6,157)
- 110マークII インシュランス フルタップ車高調
- 20,000円
- 4.8(7,694)
- ワサイハーフラック改造済+バーベルダンベルプレートセット
- 25,000円
- 4.7(4,296)
- 【特価】ハーレーダビットソン純正 アジャスタブル リアサスペンション '96-'03 XL1200S スポーツスター 54542-96A 54552-96A
16,000円- 13,600円
- 4.6(628)
- 美容師シマ様 専用です。
- 34,000円
- 4.6(8,575)
